What is an outlier in math? An outlier, in the realm of mathematics, refers to a data point that significantly deviates from the other observations in a dataset. It is an exceptional value that lies far away from the majority of the data. Outliers can arise due to various reasons, such as measurement errors, experimental anomalies, or simply due to the natural variation in the data. These intriguing outliers can provide valuable insights into the underlying patterns and characteristics of the data. They can challenge our assumptions and prompt us to question why they exist. Outliers are like the rebellious mavericks of the mathematical world, defying the norms and standing out from the crowd. They possess a certain allure that captivates mathematicians and statisticians alike, as they represent the unexpected and the unusual. Discovering and analyzing outliers can lead to new discoveries, uncover hidden relationships, and refine statistical models. By identifying and understanding outliers, we gain a deeper understanding of the data and the phenomena it represents. So, next time you encounter an outlier in your mathematical endeavors, embrace it with curiosity and delve into the mysteries it holds.
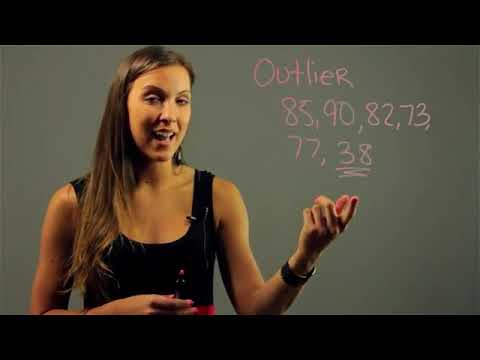
An Introduction to Outliers in Mathematics
| Outlier | Definition | Characteristics | Importance |
|---|---|---|---|
| Anomaly | An outlier, also known as an anomaly, is a data point that significantly deviates from the overall trend or pattern observed in a dataset. | – Outliers are typically located far away from the majority of the data points, either in the positive or negative direction.
– They can be observed in various statistical measures, such as mean, median, or standard deviation. – Outliers often possess unique properties that distinguish them from the rest of the data points. |
– Identifying outliers is crucial in data analysis as they can greatly impact statistical results and models.
– Outliers may indicate errors or anomalies in the data collection process, warranting further investigation. – Understanding outliers can help researchers uncover hidden patterns, relationships, or insights in the dataset. |
| Causes | Outliers can arise due to various factors, including: | – Measurement errors or data entry mistakes
– Natural variability or extreme events – Experimental or sampling bias – Data contamination or corruption |
– Identifying the causes of outliers is essential for appropriate data handling and analysis.
– Differentiating between genuine outliers and influential points is critical for accurate interpretation of results. |
| Detection | Outliers can be detected through: | – Visual inspection of data plots, such as scatter plots or box plots
– Statistical methods, such as the Z-score or modified Z-score – Robust statistical techniques, like the median absolute deviation (MAD) or the Tukey's fences |
– Utilizing appropriate detection methods is essential to ensure reliable analysis and interpretation of data.
– The choice of detection method depends on the nature of the dataset and the specific research objectives. |
| Treatment | When dealing with outliers, researchers have several options: | – Removing the outliers from the dataset, provided they are deemed as errors or irrelevant to the analysis
– Transforming the data or applying robust statistical methods that are less sensitive to outliers – Conducting separate analyses with and without the outliers to evaluate their impact on the results |
– Careful consideration must be given to the potential consequences of outlier removal or transformation.
– The chosen treatment approach should align with the research objectives and the specific characteristics of the dataset. |
Cracking the Math Code: Unveiling the Outlier Mystery
What is an Outlier in Math?
In the field of statistics, an outlier is a data point that significantly deviates from the rest of the data set. It is an observation that lies an abnormal distance away from other values. Outliers can occur by chance or indicate some underlying problem or special condition.
Identifying Outliers
To identify outliers, statisticians often use graphical methods such as scatter plots, box plots, or histograms. These visual representations help in spotting values that are far away from the majority of the data points. Additionally, statistical techniques like the z-score or the modified z-score can also be used to determine if a data point is an outlier.
The Impact of Outliers
Outliers can have a significant impact on statistical analyses and calculations. One of the main effects of outliers is that they can skew the mean of a data set. Since the mean is calculated by summing all the values and dividing by the number of values, the presence of extreme outliers can greatly influence the result. It is important to be aware of this when interpreting data.
Outliers can also affect measures of central tendency such as the median and mode. While the median is less affected by outliers as it looks at the middle value, extreme outliers may still shift its value. The mode, on the other hand, is not directly influenced by outliers since it represents the most frequently occurring value.
Furthermore, outliers can impact the accuracy of predictive models. When building a model, outliers can introduce noise and bias into the analysis, leading to inaccurate predictions. It is crucial to ensure that outliers are properly handled or removed from the data set to improve the reliability of the model.
Types of Outliers
Outliers can be categorized into three main types –
1. Univariate Outliers:
These outliers occur when a single data point in a univariate data set is exceptionally different from the others. For example, in a data set representing the heights of people, an extremely tall or short individual may be considered a univariate outlier.
2. Multivariate Outliers:
These outliers are identified in multivariate data sets, where multiple variables are considered simultaneously. Multivariate outliers occur when the combination of values for multiple variables is unusual or unexpected. Detecting these outliers requires analyzing the relationships between different variables.
3. Contextual Outliers:
Contextual outliers, also known as conditional outliers, occur when a data point is considered an outlier only in a specific context. For example, in a dataset of monthly sales, a sudden spike in sales during a holiday season may be considered a contextual outlier if it deviates significantly from the usual monthly sales.
Dealing with Outliers
Handling outliers depends on the specific context and purpose of the analysis. In some cases, outliers may represent valuable information or genuine extreme values and should not be removed. However, when outliers are due to measurement errors or data entry mistakes, it may be necessary to remove or correct them.
One approach to dealing with outliers is to transform the data using mathematical functions such as logarithms or square roots. This can help to reduce the impact of outliers and make the data more suitable for analysis.
In outlier detection, the z-score is commonly used. It measures the number of standard deviations a data point is from the mean. If a data point has a z-score greater than a certain threshold, it is considered an outlier. Another method is to use the modified z-score, which is more robust to extreme values and provides a more accurate measure of outliers.
Lastly, some statistical techniques, such as trimming or windsorizing, can be applied to remove outliers from the data set. Trimming involves removing a certain percentage of the highest and lowest values, while windsorizing replaces extreme values with a predefined upper or lower limit.
Conclusion
In summary, an outlier in math refers to a data point that significantly deviates from the rest of the data set. Outliers can have a substantial impact on statistical analyses, potentially skewing measures of central tendency and affecting predictive models. They can be categorized as univariate, multivariate, or contextual outliers, each requiring different techniques for identification and handling. Understanding and managing outliers is crucial for accurate data analysis and interpretation.
